4.具体的にどんな問題を考えているの?
本研究グループでは,現在主に以下のような問題を考えています.
- 自律分散ロボットシステムにおける問題の可解性の解明
移動可能な低機能端末(ロボットと呼ぶ)群で構成されたシステムを考えます.各ロボットは互いに区別できず,通信不可能であり,同じアルゴリズムに従って自律的に観測(Look),計算(Compute),移動(Move)のみを繰り返し実行します.これらのロボット群にあるタスク(問題)を与えたときに,「どうすれば解決できるか」それとも「解決不可能な問題であるか」などを解明します.さらに,問題が解決不可能である場合は,「どのような能力を追加すれば解決できるようになるか」なども考えます.
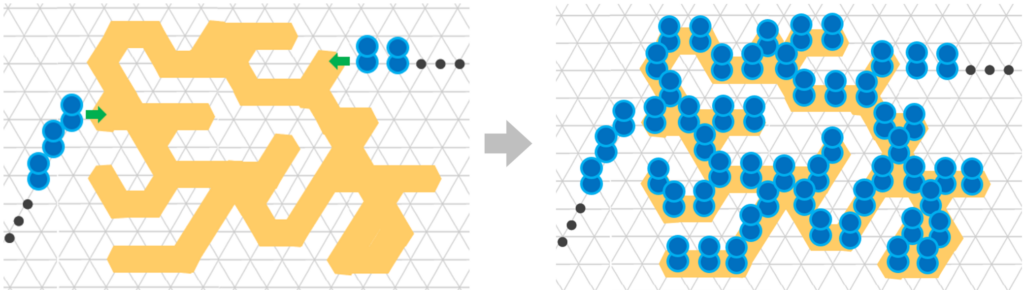
具体的にはすべてのロボットを同じ場所に集める「集合問題」,直線や四角形,円などの形状に沿って配置させる「形状形成問題」,一定の領域をロボットで隙間なく埋める「充填問題」などを扱います.
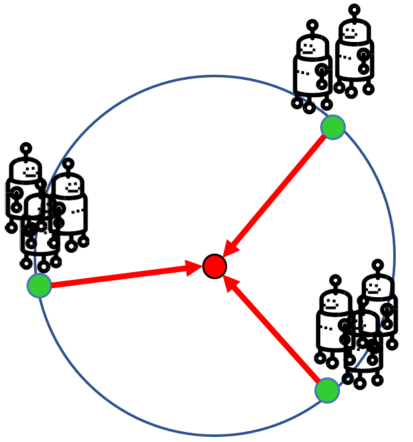
- Pairbotの計算能力の解明
自律分散ロボットシステムにおいて,予め決められた2台ロボットを一つのペア(Pair)として動作させることで問題解決能力が大きく変化することに着目し,今までのロボットで実現不可能(または困難)だった問題の解決に挑みます.ロボットは限られた視野範囲(観測可能な範囲)を持つ場合が多く,互いに観測できないほどの距離まで離れた場合は問題を解決できなくなるため,ロボット間の「連結性」はとても重要です.
ペアを組んで動作するロボット(Pairbotと呼ぶ)は,極めて限られた視野範囲であっても連結性を保ち,様々な問題が解決できるようになります.しかしながら,Pairbotに関する研究はまだ解明されていない部分が多く,沢山の課題が残っています.本研究室では,Pairbotを用いてより多くの問題の解決に挑戦し,Pairbotが持つ計算能力やその限界の解明を進めています.
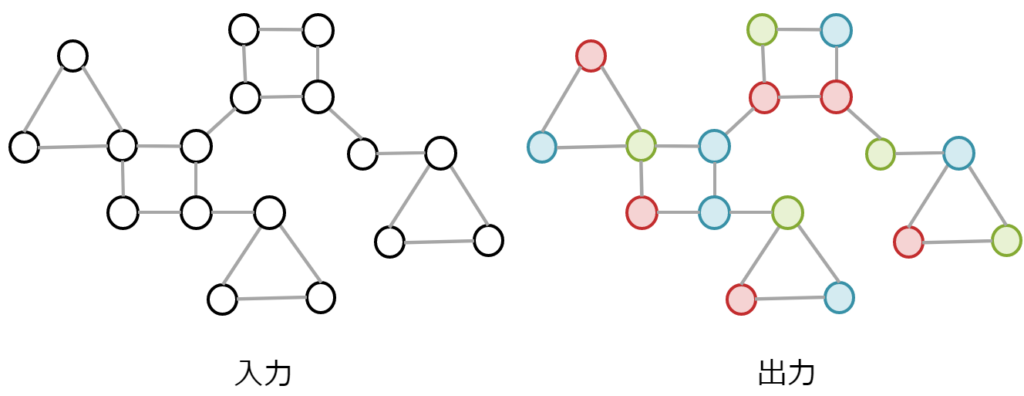
- 自己安定アルゴリズムの設計
自己安定アルゴリズムとは,任意の一時故障(リンクやノードの一時的な停止,伝搬中のメッセージの内容改変など)にかかわらず,自律的にシステムを正しい状況に戻す手法で,非常に高度な故障耐性を実現させます.現在知られている分散アルゴリズムの自己安定化を含めて,さまざまな問題に自己安定のパラダイムを適用し,高度な故障耐性を持つ分散アルゴリズムの開発を行っています.
現在取り組んでいる問題の具体例としては,「互いに素な支配集合の構築」や「頂点や辺に対するst-ordering」,「点素な通信経路の構築」など,多くの問題に取り組んでいます.
- ad-hoc ネットワークでのトークン巡回問題
ad-hoc ネットワークとは,ネットワークに接続するために特別な設定が不要で,かつネットワークへの参加・退出が自由に行えるようなものです.つまり,ネットワーク中のノードやリンクが頻繁に出現・消滅するようなネットワークモデルです.このようなネットワーク中で,トークンを安全確実に巡回させるためのアルゴリズムを開発しています. - モバイルエージェントの効率のよい巡回問題
昨今,モバイルエージェントを用いたネットワークアプリケーションがさまざま提案・実現されつつあります.たとえば,モバイルエージェントを用いてネットワーク中に存在するさまざまな情報を収集しようとするとき,エージェントをどのような戦略で巡回させれば効率よく(すばやく・確実に) 収集できるでしょうか?そのような目的のための巡回アルゴリズムの開発を行っています.
上記の問題は,あくまでも一例です.本研究グループでは,最新の論文などの輪講を行い,常に分散アルゴリズムの可能性を探っています.その過程で,他にもさまざまな問題を扱うことになります.
また,本研究グループではアプリケーションの設計,開発についても考えています.
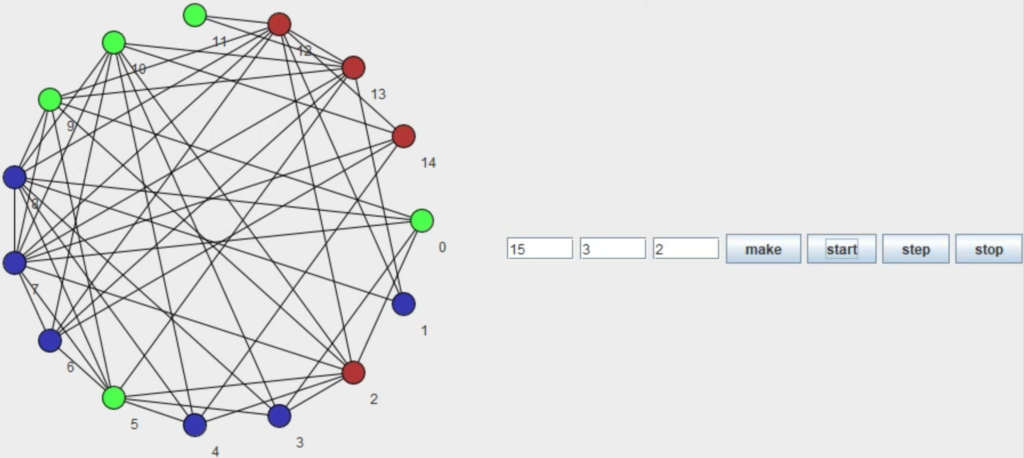
- 分散アルゴリズムの動きの可視化
分散アルゴリズムは通信リンクで互いに接続されたプロセス同士が,情報を交換し協調し問題を解くので動作は複雑になります.動画などの教材を使用して分散アルゴリズムの動きを説明しますが,この様な教材を作成するのは手間がかかります.そこで,以下の様な教材の作成を補助するツールについて設計,開発を行っています.
例えば,グラフ上で物が移動,変形する動画を作成することが可能な動画記述言語と動画生成エンジンを用いて,分散アルゴリズムの動きを示す動画を生成するツールを作成します.